← Contents

The CORE Econ website uses essential cookies to make our website work. You may disable these using your browser settings but this may affect website functionality (such as your access to logged-in resources). We would also like to use analytics cookies to help us improve the functionality of our website and improve your user experience. These analytics cookies will be set only if you accept. We do not sell or otherwise transfer personal data or usage data to any third parties or use it for any other purpose. For more detailed information about the cookies we use, see our Privacy policy.

Experiment 2 Coordination game: Investment

2.1 Introduction

CORE projects

The experiment is covered in:

Concepts in the experiment are related to material in:

What strategic considerations drive investment behaviour? How is the investment behaviour of a firm connected to the investment decisions of other firms? When deciding the level of investment, a company A considers not only its individual calculations, but also its expectations of company B’s investment. It is equally important what company A thinks about company B’s expectations of company A. In such situations, firms may coordinate on many different equilibria, and subjective factors play an important role. If investors are optimistic, they will make the investment and infect others with their optimism. If a pessimistic mood dominates, companies coordinate towards the no-investment equilibrium. That makes investments the most volatile component of aggregate demand.

The experiment in this chapter is a coordination game with an investment frame. Students are grouped in pairs and have the choice to invest or not. If both players invest, they reach the highest payoff. But if one player invests while the other does not, the investor’s payoff is reduced to zero. The experiment is played with two different framings, which students are not informed about before the experiment. Groups are told that they are investors in one of two different countries. This framing influences the investment behaviour and may promote one of the equilibria. The two countries can be chosen freely by the instructor.

Experimental evidence shows that participants find it difficult to coordinate their investment decisions but perceptions about favourable investment circumstances help to improve coordination. This finding is in line with the observation in The Economy 1.0 Figures 13.19a and 13.19b that stable investment conditions help to solve the problem of selecting between multiple equilibria. Students experience the problem of such a multiplicity and how hard coordination is in such a case. They also observe how different framings can help or hinder coordination. They can use these insights to explain the volatility of investments in the real world.

You may find it useful to read about the experiences of instructors before getting into the detail of setting up the experiment, especially if you are new to running classroom experiments.

The experiment is based on Johann Graf Lambsdorff and Marcus Giamattei. 2020. Macroeconomics. Lecture in Economics.

Citation

Giamattei, Marcus, Johann Graf Lambsdorff and Humberto Llavador (2021). ‘Coordination game: Investment’. Experiment 2 in The CORE Team, Experiencing Economics. Available at https://www.core-econ.org/experiencing-economics [Accessed on (date)].

Key concepts

This experiment will help students understand the following key concepts:

  • Coordination game
  • Volatility of investments
  • Expectations
  • Multiple Nash equilibria

2.2 Requirements

Timing

The game is very short as it only consists of one decision made by each participant. It can be run in 10 minutes (including some introductory explanation). Remember to allow time for a stimulating discussion.

Resources

Instructors and students need a smartphone, tablet, or laptop that has a web browser and is connected to the Internet. For in-class experiments, a projector is recommended to help with instructions, results, and discussion. The experiment will be run in classEx.

2.3 Description of the experiment

In this experiment, students are grouped into pairs. Each student has to decide whether to invest or not. If both players invest, they reach a high payoff. Not investing always yields a low payoff, whether or not the other player invests. But if one player invests while the other does not, the investor’s payoff is reduced to zero. This resembles a standard coordination game with two possible equilibria (both invest or both do not invest). While mutual investment is Pareto efficient, the risk of miscoordination may lead to investors ending up in the low payoff equilibrium.

2.4 Step-by-step guide

Detailed instructions

Go to the ‘Quick summary’ section if you have previously run the experiment and just need a brief reminder of the instructions.

  1. Enter the ‘Investment Game’ in the ‘CORE’ tab in classEx. Click ‘Play’.
  2. Check that the parameters correspond to your settings. This section uses the default settings (Figure 2.1). Change the country names according to your own needs. Make sure you change the country names before class as students should not be made aware of the two scenarios. See the ‘Advanced settings’ section for details if you want to change any of the other parameters.

2.5 Student instructions

These are also available in the students’ version.

A PDF of the student instructions and homework questions is also available.

Please note that the payoffs are based on the standard parameters. If you intend to change the payoff parameters you will need to adapt the instructions. If you only want to change the country names you can use the student instructions provided here.

You will be put into groups of two and assigned as either a red player (the red player ) or a green player (the green player ). You will both simultaneously decide whether to invest or not. Your return on investment depends on the decision taken by the other player as shown in the matrix in Figure A.

Rows show the available options for the red player , and columns the available options for the green player . The cells show the respective payoffs for both players according to their decision. For example, in the first row and first column you can find the payoffs if both invest. The following combinations are possible:

Matrix summarizing the payoffs.

Figure A Matrix summarizing the payoffs.

  • If the red player and the green player both invest, both get 10.
  • If the red player and the green player both do not invest, both get 5.
  • If the red player invests, but the green player does not, the red player gets 0 and the green player gets 5.
  • If the red player does not invest, but the green player does, the red player gets 5 and the green player gets 0.

Once the experiment has been started, the decision screen appears on your device (see Figure B for an example). In the top row, you can see whether you are the red player or the green player . You can make your decision by pressing the button ‘Invest’ or ‘Do not invest’. The decision is executed immediately so think carefully before making your decision.

Decision screen

Figure B Decision screen

Once all participants have made their decision, the instructor ends the experiment and the feedback is shown on your screen. Figure C shows an example.

Example of a feedback screen when no player invests.

Figure C Example of a feedback screen when no player invests.

In Figure C, you can see your decision in the first row (for example, here ‘Do not invest’) together with your payoff. In the second row, you can see the decision and the respective payoff of the other player.

How to interpret the payoffs

Here we provide some information on how to interpret the payoffs, but you can skip this information as it is not necessary to play the game.

The payoffs in the game can be justified by thinking of two firms who want to invest into a new technology that will only be successful if both firms invest. Otherwise there will not be enough demand for the new product nor will it be worth building up the infrastructure to deploy the products. They have an endowment of 5. If only one firm invests but the other does not, the product is not successful and the firm who invested loses its endowment. The firm therefore ends up with a payoff of 0. The firm who did not invest keeps its original endowment of 5. The same is true if they both keep their endowment.

2.6 Predictions

Predicted results

At the end of the experiment, you will see the results within the decision matrix. You can expect to obtain something similar to the graphs in Figure 2.7, which show the results from the reference example in classEx: an experiment run with a class of 540 students at the University of Passau (Germany) in 2020.

2.7 Discussion

A good discussion following the experiment is important. Ask your students the following questions to frame the discussion.

Interpreting the graphs

Comments in the ‘What might go differently’ section provide useful further information.

2.8 Homework questions

These questions can be set for students to work on outside the classroom or can be completed and discussed in the classroom. They may help students reflect on their experience and understand their and others’ behaviour in the experiment.

For question 2, you have to share a screenshot of the results screen with your students. If your results screen does not show the predicted results, you can use Figure 2.7 and share it with the students.

Data from your experiment can be downloaded as an Excel file from the ‘data’ menu in the instructor’s screen in classEx. You can use this data to create your own questions. A description of the data variables can be found in the ‘Downloading the data from your experiment’ section.

The following text is also available in the students’ version.

  1. Explain the following concepts, referring to your experience from the game played in class:
    1. Multiple equilibria in a coordination game.
    2. How the attractiveness of investments depends on the investments of others.
    3. The role of expectations in decision making.
  2. Your instructor shared with you the results for the investment game that you played.
    1. What equilibria are there in the game? How do expectations regarding the other player’s decision affect one’s own investment decision?
    2. In the lecture, the participants were given private information. This information does not change the payoffs in the game. Nevertheless, it turns out that investments are more frequent in some circumstances. Explain this result. How can the results help to explain that investments are volatile in an economy?
    3. Critically discuss the fact that the game has been run in your home country.
  3. Figure D (Figure 13.17 from The Economy 1.0) shows the payoffs in an investment game.
    1. Explain how the payoffs in the game relate to the investment decisions of two firms.
    2. What are the Nash equilibria in the game? Define the concept of Nash equilibrium as well. How do expectations regarding the other player’s decision affect one’s own investment decision?
    3. Given your experience of the game in class, how would the theoretical solution differ from the expected outcome if the game were played by students?
    4. Imagine the game is played with a value of 10 instead of the −40. What changes do you expect in the behaviour of participants? Why?
    5. Describe other factors, besides the investment decision of other firms, that investment decisions are based on.
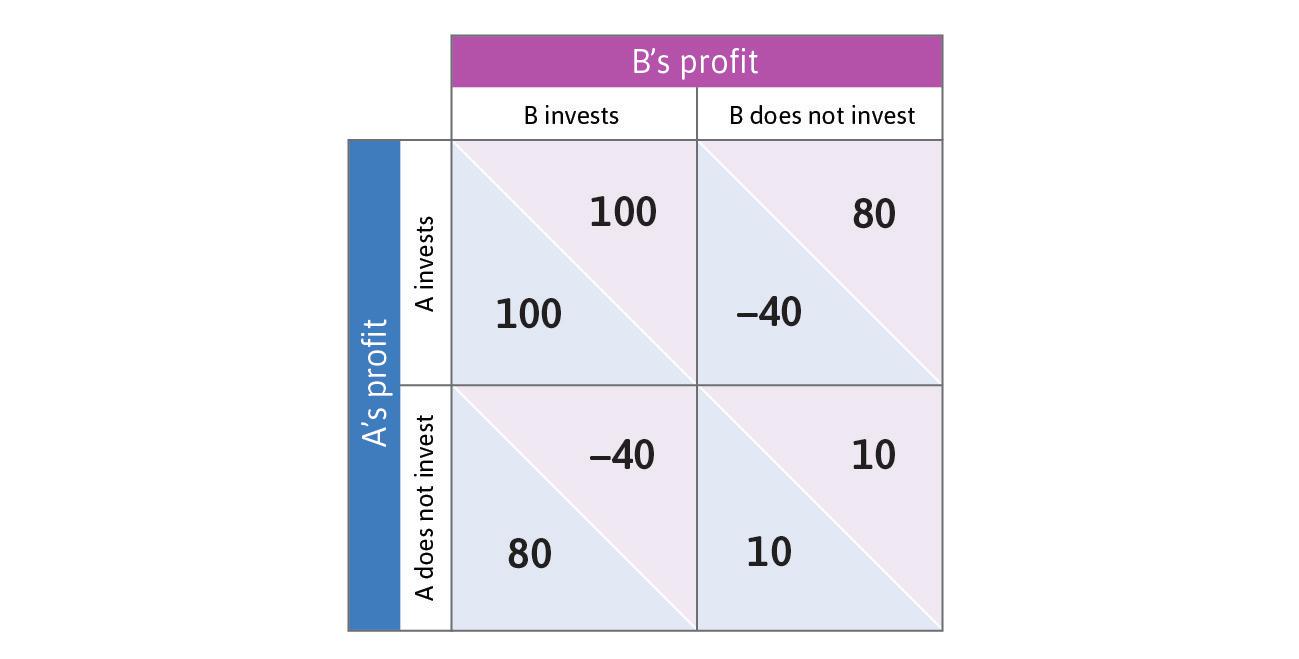
Figure 13.17 from The Economy 1.0, showing payoffs in a coordination game.

Figure D Figure 13.17 from The Economy 1.0, showing payoffs in a coordination game.

  1. Think back to the investment game that you played in class.
    1. What factors can help to stabilize investment decisions within a country?
    2. What is the role of the government and of industrial representatives here?

2.9 Further reading

Also available in the students’ version.

  • Akerlof, G. and Shiller, R.J. Animal spirits: How human psychology drives the economy, and why it matters for global capitalism. 9th edition. Princeton University Press, 2010, pp. 131-148.
  • Barrera, C. Blockchain and Coordination Games: Failures and Focal Points. 2018.
  • CORE The Economy 2.0: Microeconomics, Section 4.13.
  • CORE The Economy 1.0, Sections 13.7, 4.13 and 21.3.
  • CORE Economy, Society, and Public Policy, Section 2.12.
  • Mielke, J. and Steudle, G.A. Green Investment and Coordination Failure: An Investors’ Perspective, Ecological Economics, 150, 2018, pp. 88-95.
  • Soskice, D. and Carlin, W. Macroeconomics: Institutions, Instability, and the Financial System. Oxford University Press, 2014, pp. 29-32.

2.10 Instructor experience

In this section, we hear from instructors about their experience of running the experiment with their students.