Experiment 6 The conflict game
6.1 Introduction
CORE projects
Concepts in the experiment are related to the material in:
In a two-person negotiation, should people be competitive or try to cooperate with each other to get a better result? How do negotiators’ incentives affect the ease with which an agreement can be reached? When conflict between the interests of both parties increases, are people more likely to negotiate aggressively or peacefully? Conflict and bargaining are closely related in various everyday situations. Political parties clash for government control, unions go on strike, legal disputes end up in court, and firms compete in aggressive price wars. Not all negotiations have the same level of conflict. Some situations are simple, such as couples’ arguments over the distribution of tasks, and others are much more complex, such as clashes between nations to define trade agreement conditions.
For simplicity, we can say there are two ways of approaching a negotiation: being a Hawk or a Dove. In this metaphor, negotiating as a Hawk is to approach conflict aggressively and selfishly, putting personal interests above those of the group. In contrast, acting as a Dove implies seeking the common good and preferring cooperative relationships. Arguably, we do not behave the same way all the time, in all situations. Therefore, analysing the conditions that favour selfish behaviour and under what conditions cooperation flourishes is exciting. The discussion about the conflict between cooperation and self-interest is covered in Section 4.10 of The Economy 2.0: Microeconomics (Section 4.9 of The Economy 1.0).
This game addresses questions of cooperative and competitive behaviour, and facilitates the explanation of Nash equilibrium and other basic game theory concepts. The learning objective is to understand how incentives affect individuals’ bargaining decisions.
The experimental protocol uses a stylized model that captures different levels of preference alignment. It is inspired by the 2×2 conflict game originally proposed by Baliga and Sjöström (2004), discussed extensively in Palacio, Cortés, and Muñoz (2015).
Citation: Palacio García, Luis Alejandro and Daniel Parra. 2023. ‘The conflict game’. Experiment 6 in The CORE Team, Experiencing Economics. Available at https://tinyco.re/7564028.
Key concepts
This experiment will help students understand the following key concepts:
- Nash equilibrium
- Efficiency
- Coordination
- Cooperation
- Negotiation.
6.2 Requirements
Timing
The game is quick to run as it only consists of one decision made by each participant, in each of the five rounds. Explaining the game and running five rounds takes about 20 minutes. Remember to allow time for a stimulating discussion.
6.3 Description of the experiment
There are two types of players, Blue and Green, who make their decisions simultaneously, choosing between two alternatives, Dove or Hawk. The payoffs may be interpreted as the outcomes of a couple negotiating how to split a prize worth 2000. Each one can negotiate as a Dove or as a Hawk. Therefore, there are three possible outcomes:
- If both negotiate like a Dove, they do not confront each other and they split the prize equally.
- If both negotiate like a Hawk, they will fight fiercely, hurting each other, and getting only 250 each.
- If one negotiates like a Hawk and the other like a Dove, the Hawk gets a prize of \(Y\), while the Dove gets \(X\).
6.4 Step-by-step guide
Detailed instructions
Go to the ‘Quick summary’ section if you have previously run the experiment and just need a brief reminder of the instructions.
6.5 Student instructions
These instructions are also available in the students’ version.
A PDF of the student instructions and homework questions is also available.
Introduction
In this game, you will play five rounds. In each round, you will be randomly matched with another student and you both will have to decide simultaneously how to behave in negotiating a deal worth 2000: cooperatively (as a Dove) or aggressively (as a Hawk). At the end of the round, you will receive a payoff according to the information in the payoff matrix (see Figure A for an example).
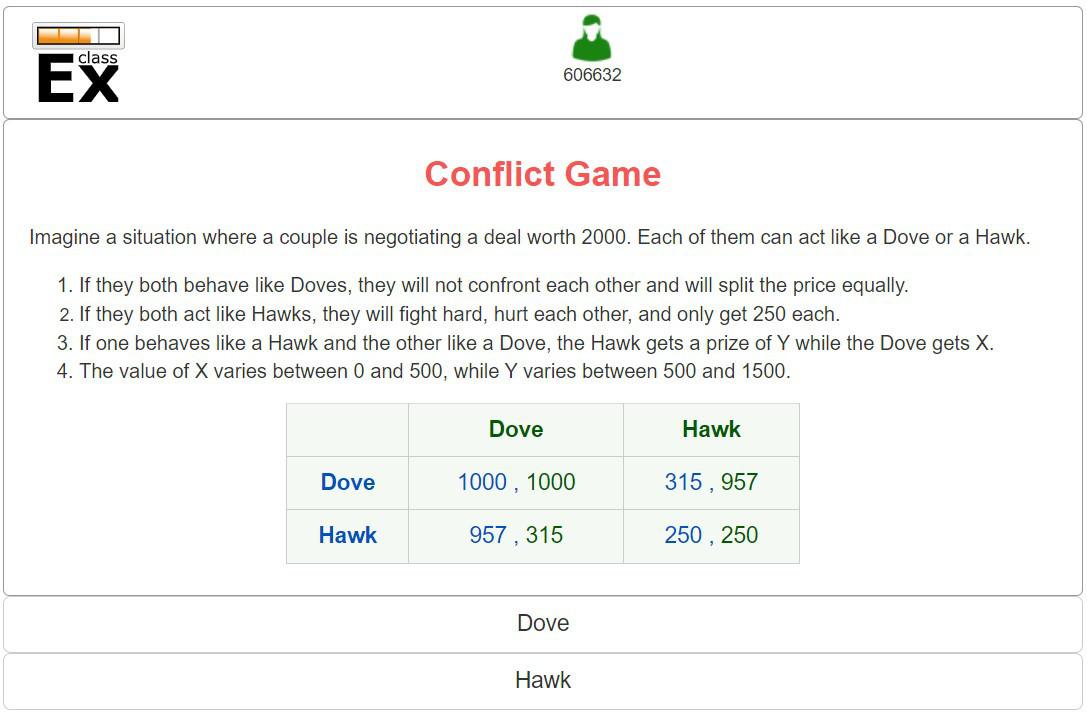
Figure A Students’ screen for a realization of \(X=315\) and \(Y=957\).
Observe that in each round, you might play with a different student who will be randomly selected from all participants; and that sometimes you will be the Blue player and at other times the Green player. Finally, recall that you will both decide simultaneously and you will play five rounds.
Profits
Profits are calculated using the two variables, \(X\) and \(Y\). The value of \(X\) will always be a random number between 0 and 500, and that of \(Y\) will be a random number between 500 and 1500. They will take a different value at the beginning of each round and participants will know the round’s value before they decide.
Note that there are three possible payoff combinations. At the end of the experiment, you will earn the sum of the profits of all the rounds.
- If both students in the pair behave as a Dove, they will not fight and will therefore split the 2000 prize equally.
- If both behave as a Hawk, they will fight fiercely, hurting each other and getting only 250 each.
- If one behaves as a Hawk and the other as a Dove, then the Hawk gets a prize of \(Y\), while the Dove gets \(X\).
Figure B shows this explanation and other details that will be shown in your instructor’s screen.

Figure B Instructor screen.
6.6 Predictions
Predicted results
The game has four different scenarios that depend on the \(X\) and \(Y\) values. In other words, this meta-game contains four different games (scenarios): C1. Dominant Dove: \(Y<1000\) and \(X>250\); C2. Strategic complements (stag hunt): \(Y<1000\) and \(X<250\); C3. Strategic substitutes (chicken): \(Y>1000\) and \(X>250\); and C4. Dominant Hawk (prisoners’ dilemma): \(Y>1000\) and \(X<250\).
6.7 Discussion
A good discussion following the experiment is essential. Ask your students the following questions to frame the discussion.
Reflecting on the decisions that players made
- Should we always consider the other a rival when facing a negotiation?
- Does successfully negotiating imply winning, or is it about seeking cooperation?
The metaphor of Dove and Hawk as a way of approaching negotiation has proved very useful in facilitating an understanding of the game. Students quickly understand that they should not always act the same way in all situations because incentives may change from one situation to another.
Additionally, these strategies can be thought of as personality characteristics. For simplicity’s sake, one can say that some people are prone to behave like Doves, seeking cooperation. On the other hand, some tend to behave like Hawks, which is understood as a more competitive personality.
Interpreting the graphs
The group discussion can be advanced by analysing the aggregated results over several rounds as an approximation to the equilibria of each game. To better understand the collective phenomenon, it is necessary to investigate the data collected in the experiment in greater detail. At the end of the session, discuss the following two guiding questions with the students:
- Are students willing to cooperate depending on the level of conflict they are facing?
- Is the decision to be a Dove affected by the value of \(X\) and \(Y\)?
Using the data, the guiding questions can be answered by observing the proportion of students who decide to play cooperatively as Doves as a function of the level of conflict. Figure 6.10 is an example of the graph showing the students’ decisions in the four different scenarios of the conflict game. Using this graph, the instructor can show that cooperation is easier when there are lower levels of conflict. This graph is automatically generated by classEx. Exploring these graphs in the classroom after playing the conflict game would enrich all the discussions. The graph shows that the higher the level of conflict, the more likely it is that students use the Hawk strategy.
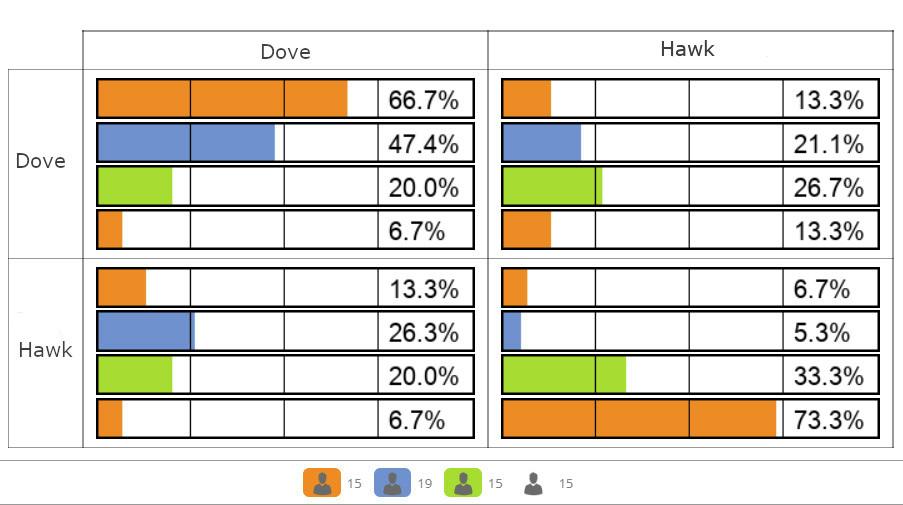
Figure 6.10 Four levels of conflict as a function of the \(Y-X\) parameter. The first orange bar represents C1, the blue bar represents C2, the green bar represents C3, and the last one represents C4. Data from classroom experiment at Universidad Industrial de Santander, Bucaramanga-Colombia. Microeconomics II 2022 I.
Relating the experiment to real life
- Can you identify an example of a real-life situation like the one you just played? This experience aims to analyse how external conditions and the environment around us can affect individual decisions. This game allows us to understand and discuss the effect of the level of conflict on the decision to cooperate. The higher the level of conflict, the greater the incentive for participants to act aggressively.
To help the students identify relevant everyday situations, the following questions can be asked:
- Does a negotiator act aggressively depending on the environment?
- Are there environments where it is easy to cooperate and others where people are more aggressive?
To identify the level of conflict, students are asked to reflect on different negotiations they see in their daily lives. Not all contexts are the same: some negotiations are simple, and others are much more complex. The aim is to understand strategic interaction and how people respond to incentives. This forces us to consider the systemic problem, where there are interrelationships between individual decisions and collective welfare.
Additionally, in everyday life, there are several situations in which it is necessary to coordinate the decisions of different people. Although it may sometimes seem easy, conflicting incentives can make it difficult to coincide. In coordination games, agents have several options, and the payoff is higher if they all agree on a particular action. Therefore, it is essential to analyse when and how coordination can be improved, understanding the conflict as a series of negotiations, offers, and counteroffers to characterize optimal strategies. This implies stressing the idea that, in addition to divergent interests, there is a powerful common interest in reaching a solution that avoids falling to the point of disagreement.
Link to theory
Thomas Schelling, winner of the Nobel Prize in Economics in 2005, studied negotiation as a process in which parties seek to reach agreements that benefit them individually. His ideas have had a great impact on economics and other disciplines such as political science and international relations.
In this context, game theory has been used to explore decision-making in conflict situations. The conflict game is an example of this. The proposed protocol makes it possible to analyse how external conditions and the environment can influence individual decisions, determining the level of conflict.
The level of conflict is expected to affect the decision to cooperate. In this sense, the main question that arises is whether participants are willing to cooperate as a function of the level of conflict they face. When conflict is higher, participants are likely to have greater incentives to act aggressively rather than cooperatively.
The instructor can guide the participants during the game to reach their own conclusions. Guiding questions include:
- How do you think the level of conflict can influence people’s willingness to cooperate?
- Can you think of examples of real-life situations where the level of conflict affects decisions to cooperate?
Critical evaluation of the experiment
- What assumptions were used in the experiment?
- How do these assumptions compare with real-life situations?
- Can the level of conflict in a negotiation be measured?
- Do you think the behaviour would change if it were played with real money?
- Do you think the behaviour would change if played in different cultures?
6.8 Homework questions
These questions can be set for students to work on outside the classroom or can be completed and discussed in the classroom. They may help students reflect on their experience and understand their own and others’ behaviour in the experiment.
Data from your experiment can be downloaded as an Excel file from the ‘data’ menu on the instructors screen in classEx. You can use this data to create your own questions. A description of the data variables can be found in the ‘Downloading the data from your experiment’ section.
This experiment complements the lectures and workshop exercises of a first game theory class. Those studying Unit 4 in The Economy 2.0: Microeconomics (Unit 4 in The Economy 1.0) will find this game particularly helpful. Specifically, it is a design that allows modelling different levels of conflict, where classic dilemmas such as the stag hunt, the chicken, and the prisoners’ dilemma are considered as particular cases. The following is an exercise to be carried out in the form of a theoretical problem set to reinforce the concepts related to game theory.
The following text is also available in the students’ version.
The conflict game
There are two players: Blue and Green. Blue will choose between Dove and Hawk and Green between Dove and Hawk. Both will make their decision simultaneously. The payoffs are represented in Figure C. In addition, there are two variables, \(X\) and \(Y\). The value of \(X\) will always be a number between 0 and 500, and the value of \(Y\) will always be a number between 500 and 1500.
| Dove | Hawk | |
|---|---|---|
| Dove | 1000 , 1000 | X , Y |
| Hawk | Y , X | 250 , 250 |
Figure C Payoff matrix.
- Represent the following four games in normal form and then find the Nash equilibria:
- \(Y\) < 1000 and \(X\) > 250
- \(Y\) < 1000 and \(X\) < 250
- \(Y\) > 1000 and \(X\) > 250
- \(Y\) > 1000 and \(X\) < 250.
- Represent the above four games in their extensive (sequential) form with perfect information and find the perfect Nash equilibrium in subgames.
- Clearly define a way to measure conflict in this game by a quantitative variable. Explain your answer.
6.9 Further reading
Also available in the students’ version.
- ‘The Disturbing New Relevance of Theories of Nuclear Deterrence’ (The Economist, 18 March 2022) describes how Schelling’s game-theoretic analysis helps to understand the conflict in Ukraine and the nuclear brinkmanship between Russia and the West.
- ‘What the Protracted Game of Chicken Over First Republic Tells Us’ (Financial Times, 1 May 2023) uses the game of chicken to explain the protracted stand-off between the two banks, where each side hopes the other will blink first and give up or compromise.
- ‘An Essay on Bargaining’ (Schelling, 1956) presents a theory of conflict and cooperation.
- ‘The Strategy of Manipulating Conflict’ (Baliga & Sjöström, 2004) presents the original 2×2 conflict game.
- ‘The Strategic Role of Nonbinding Communication’ (Palacio et al., 2015) extensively discusses the conflict game, where the discussion of the Nash equilibrium concept is addressed in different bargaining contexts.
6.10 Instructor experience
In this section, we hear from instructors about their experience running the experiment with their students.


