Unidad 7 La empresa y sus clientes
7.2 Cereales para el desayuno: escoger un precio
¿Cómo decide una empresa el precio que cobra por su producto? Para maximizar el beneficio, debe estudiar el precio al que puede vender el producto y la cantidad que debería producir, teniendo en cuenta sus costes de producción.
Ingresos, costes y beneficio
Los primeros cereales listos para el desayuno, Kellogg’s Corn Flakes y Quaker Oats’ Puffed Rice, empezaron a venderse en Estados Unidos en los primeros años del siglo XX. Ahora existen miles de diferentes cereales; a nivel mundial, el sector estaba valorado en más de 90 000 millones de dólares en 2020.
Imagina una empresa que crea y vende una marca de cereales para el desayuno.
- costes totales
- Suma de todos los costes que conlleva para una empresa la producción de todos sus productos.
- ingresos, ingresos totales
- Número de unidades que vende una empresa multiplicado por el precio de cada unidad.
El beneficio es la diferencia entre los ingresos que percibe por la venta de los cereales y los costes de producirlos. Supón que el coste unitario de elaboración es de 2 dólares por cada libra de peso (1 libra = 454 gramos). Si cada semana produce Q libras y las vende a un precio de P, podemos calcular los costes totales, los ingresos y el beneficio:
\[\begin{align*} \text{costes totales} &= \text{coste unitario} \times \text{cantidad} \\ &= 2 \times Q \\ \text{ingresos totales} &= \text{precio} \times \text{cantidad} \\ &= P \times Q \\ \text{beneficio} &= \text{ingresos totales} - \text{costes totales} \\ &= (P \times Q) - (2 \times Q) \end{align*}\]Así obtenemos una fórmula para el beneficio:
\[\text{beneficio} = (P-2) \times Q\]y podemos calcular el beneficio que la empresa obtendría si pudiera vender Q libras al precio de P. Por ejemplo, si P = 4 y Q = 50 000, beneficio = 100 000.
La figura 7.2a muestra representaciones tridimensionales de cómo el beneficio depende de Q y de P. Cada punto de la cuadrícula horizontal corresponde a una combinación específica de (Q, P). La altura de la superficie coloreada mostrada por encima de la cuadrícula representa el beneficio que se obtiene en cada punto. El beneficio forma una «montaña», cuya altura empieza en cero donde Q = 0 y P = 2 (el precio es igual al coste unitario). A medida que aumentan P y Q, también lo hace el beneficio. Hemos trazado curvas de nivel que unen los puntos de la misma altura (mismo beneficio): el punto donde P = 4 y Q = 50 000 está en la curva del nivel 100 000.
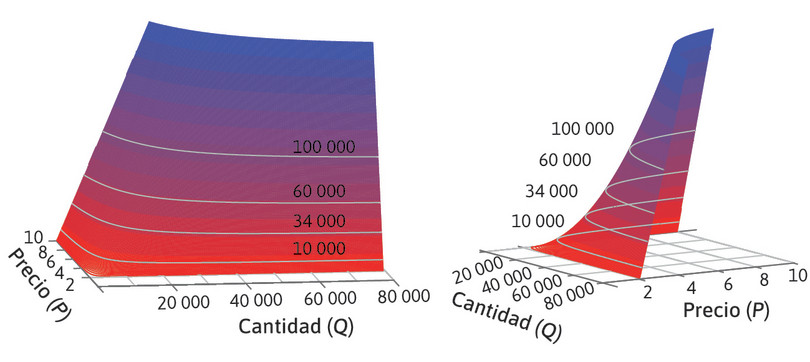
Figura 7.2a Beneficio como función del precio y la cantidad de una empresa cuando el coste unitario es 2.
- curva de isobeneficio
- Curva que relaciona las combinaciones de precios y cantidades de un bien que a una empresa le generan los mismos beneficios.
- curva de indiferencia
- Curva que une todas las combinaciones de bienes que proporcionan un nivel determinado de utilidad al individuo.
En la figura 7.2b, representamos el beneficio en dos dimensiones dibujando las curvas de nivel de la «montaña» del beneficio sobre la cuadrícula (Q, P). Las llamamos curvas de isobeneficio (isobeneficio significa ‘mismo beneficio’): unen todos los puntos (Q, P) que generan el mismo nivel de beneficio.
Las curvas de isobeneficio podríamos describirlas como las curvas de indiferencia de la empresa, es decir, a la empresa le resulta indiferente cualquier combinación de precio y cantidad que le genere el mismo nivel de beneficio.
Pregunta 7.1 Elige las respuestas que sean correctas
El coste de producción de una empresa es de 12 £ por unidad de producción. P es el precio del bien producido y Q es la cantidad de unidades producidas. Partiendo de esta información, lee los siguientes enunciados y elige los que sean correctos.
- En (Q, P) = (2000, 20), el beneficio = (20 – 12) × 2000 = 16 000 £.
- En (Q, P) = (2000, 20), el beneficio = (20 – 12) × 2000 = 16 000 £. En (Q, P) = (1200, 24), el beneficio = (24 – 12) × 1200 = 14 400 £. Por lo tanto, (2000, 20) está en una curva de isobeneficio más alta.
- En (Q, P) = (2000, 20), el beneficio = (20 – 12) × 2000 = 16 000 £. En (Q, P) = (4000, 16), el beneficio = (16 – 12) × 4000 = 16 000 £. Por lo tanto, esos dos puntos se encuentran en la misma curva de isobeneficio.
- En P = 12 la empresa no obtiene ningún beneficio. Por lo tanto, (5000, 12) estará en la curva de isobeneficio horizontal que representa un beneficio cero.
Pregunta 7.2 Elige las respuestas que sean correctas
Piensa en una empresa cuyo coste unitario (el coste de producir una unidad de un bien) es el mismo con independencia de cual sea la cantidad de bienes producidos. Partiendo de esta información, lee los siguientes enunciados y elige los que sean correctos.
- Una curva de isobeneficio une todas las combinaciones de precio y producción en las que el beneficio de la empresa es el mismo.
- Si el beneficio es alto, el precio debe estar por encima del coste unitario. Entonces, si se aumenta la producción, el precio tiene que reducirse para que el nivel de beneficio se mantenga constante. Por lo tanto, las curvas de isobeneficio deben tener pendiente negativa.
- Es posible calcular el beneficio para cualquier combinación de precio y cantidad y, hallando otros puntos que generen el mismo beneficio, trazar una curva de isobeneficio que pase por todas esas combinaciones.
- Si el precio está por encima del coste unitario y se aumenta la producción, el precio debe reducirse para mantener constante el beneficio, por lo que la curva de isobeneficio tiene pendiente negativa.
Demanda
A la empresa le interesa que tanto el precio como la cantidad sean altos. Pero, si pone el precio demasiado elevado, nadie querrá comprar. Por eso, necesita información sobre la demanda: cuánto están dispuestos a pagar los posibles consumidores.
- curva de demanda
- Una curva de demanda muestra el número de unidades de un bien que los compradores querrían adquirir a cada precio dado. También denominada: función de demanda.
La figura 7.3 muestra la curva de demanda de Apple Cinnamon Cheerios, una marca de cereales listos para el desayuno que la empresa General Mills lanzó al mercado en 1989. En 1996, el economista Jerry Hausman utilizó datos de ventas semanales de cereales para el desayuno en distintas ciudades estadounidenses para estimar cómo variaría la cantidad de cereales que los consumidores comprarían cada semana si cambiase su precio, expresado en dólares por libra. Por ejemplo, la figura 7.3 muestra que, si el precio fuera de 3 dólares, los consumidores demandarían 25 000 libras de Apple Cinnamon Cheerios. Con la mayoría de los productos, cuanto más bajo es el precio, más quieren comprar los clientes.

Figura 7.3 Demanda estimada de Apple Cinnamon Cheerios.
Adaptación de la figura 5.2 publicada en: Jerry A. Hausman. 1996. «Valuation of New Goods under Perfect and Imperfect Competition». The Economics of New Goods. Chicago, IL: University of Chicago Press. pp. 207–248.
La economía aprende de los hechos Estimación de curvas de demanda a partir de encuestas
Jerry Hausman se sirvió de datos de compras de cereales para estimar la curva de demanda de Apple Cinnamon Cheerios. Otro método, que resulta especialmente útil para las empresas que lanzan productos completamente nuevos, consiste en encuestar a los consumidores. Supón que estás investigando la posible demanda del turismo espacial. Podrías probar a preguntarles a los consumidores potenciales:
«¿Cuánto pagaría por un vuelo de diez minutos al espacio?».
Sin embargo, es posible que les sea difícil decidirse o, peor aún, que opten por mentir si creen que su respuesta va a afectar al precio que con el tiempo tendrán que pagar. Una forma más conveniente de averiguar cuánto estarían dispuestos a pagar en realidad podría ser preguntar:
«¿Pagaría 1000 dólares por un vuelo de diez minutos al espacio?».
Cuando esta pregunta se planteó en 2011, un 24,6 % de las personas encuestadas respondió que sí.1
Da igual si el producto son cereales o vuelos espaciales, el método es el mismo. Si cambias los precios de la pregunta y encuestas a un gran número de consumidores, puedes estimar la proporción de personas dispuestas a pagar cada precio y, por tanto, la curva de demanda entera.
Maximización del beneficio
Si dirigieras General Mills, ¿cómo establecerías el precio de Apple Cinnamon Cheerios y cuánta cantidad de cereales producirías?
Supondremos que el coste unitario de Apple Cinnamon Cheerios es de 2 dólares. Entonces:
- Las curvas de indiferencia son las mostradas en la figura 7.2b. Para lograr un beneficio elevado, es preferible que tanto P como Q sean lo más altos posible.
- Pero la curva de demanda constituye un factor limitador (figura 7.3), ya que determina lo que es factible. En ella se muestra el número de consumidores de Apple Cinnamon Cheerios que están dispuestos a comprar a cada precio dado. Si pones un precio alto, solo podrás vender una cantidad pequeña, por lo que deberás poner uno más bajo si quieres vender una cantidad mayor.
La figura 7.4a muestra juntas las curvas de isobeneficio y la curva de demanda. Aquí te enfrentas a un problema similar a Karim, el trabajador de la unidad 3 que quiere elegir el punto de su conjunto factible donde la utilidad sea máxima. Lo que buscas es escoger una combinación factible de precio y cantidad que maximice tu beneficio.
La mejor estrategia es elegir el punto E de la figura 7.4a. Así, producirás 15 000 libras de cereales y las venderás a razón de 4,23 dólares por libra, lo cual te reportará un beneficio de 33 450 dólares.
- problema de elección restringida
- Problema que obliga a elegir los valores de una o más variables para alcanzar un objetivo (como maximizar el beneficio o la utilidad) teniendo en cuenta alguna restricción que condiciona el conjunto de opciones factibles (como la curva de demanda o la restricción presupuestaria).
Maximizar el beneficio es un problema de elección restringida, que tiene la misma estructura que la elección de Karim sobre las horas de trabajo en la unidad 3.
- Quien toma las decisiones quiere escoger los valores de una o más variables que le permitan lograr un objetivo. En el caso de Apple Cinnamon Cheerios, las variables son el precio y la cantidad; en el de Karim, son el consumo y el tiempo libre.
- El objetivo es optimizar algo: el trabajador busca la máxima utilidad y la empresa, el máximo beneficio; en otros modelos, la empresa podría buscar minimizar los costes.
- Quien tiene que tomar la decisión se enfrenta a una restricción que limita lo que resulta factible: la restricción presupuestaria para Karim; la curva de demanda para Apple Cinnamon Cheerios.
En cada uno de estos casos, hemos representado la elección de forma gráfica, utilizando curvas de indiferencia que reflejan el objetivo (utilidad o beneficio) y dibujando el conjunto factible de resultados que viene determinado por la restricción. Y hemos identificado que la solución al problema se sitúa en el punto de tangencia entre las curvas de indiferencia y la restricción.
Elección restringida
Al ir a tomar una decisión, se elige el valor de una o más variables
- … para establecer un objetivo
- … en función de una restricción que determina el conjunto factible.
Cuando diriges la empresa pensando en el beneficio, tu elección debe buscar un equilibrio entre el precio y la cantidad, el cual está condicionado por dos limitaciones:
- La restricción que te impone la curva de demanda.
- La disposición que tengas a que te limite la curva de isobeneficio (donde todos los puntos te dan el mismo beneficio).
Es probable que los responsables de General Mills no se planteasen la decisión de esta forma.
Tal vez se fijó el precio más por el método de ensayo y error, a partir de experiencias pasadas y de estudios de mercado. Sin embargo, es de esperar que, de un modo u otro, una empresa acabe dando con el precio y la cantidad que maximicen el beneficio. El propósito de nuestro análisis económico no es hacer un modelo del proceso mental del director general, sino entender el resultado y cómo depende de los costes que soporta la empresa y de la demanda de los consumidores.
Incluso para un economista, existen otras maneras de concebir la maximización del beneficio. En la figura 7.4b, hemos calculado cuánto beneficio se obtendría en cada punto de la curva de demanda con el fin de averiguar en cuál es mayor.
El gráfico del panel inferior es la función de beneficio y muestra el beneficio que se obtendría si se decidiera producir una cantidad, Q, y se fijara el precio más alto que permitiría vender esa cantidad. Una vez más, nos confirma que el beneficio máximo estaría en el punto E.
Pregunta 7.3 Elige las respuestas que sean correctas
La tabla representa la demanda Q de un bien a diferentes precios P.
| Q | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| P | 270 £ | 240 £ | 210 £ | 180 £ | 150 £ | 120 £ | 90 £ | 60 £ | 30 £ | 0 £ |
El coste unitario de producción para la empresa es de 60 £. Partiendo de esta información, lee los siguientes enunciados y elige los que sean correctos.
- En Q = 100, el beneficio = (270 − 60) × 100 = 21 000 £.
- En Q = 400, el beneficio = (180 − 60) × 400 = 48 000 £. Si calculas el beneficio para cada punto de la curva de demanda, verás que es más bajo en los demás puntos.
- El beneficio es el mismo en ambos puntos: En Q = 300, el beneficio = (210 − 60) × 300 = 45 000 £. En Q = 500, el beneficio = (150 − 60) × 500 = 45 000 £.
- La empresa tendrá pérdidas (beneficio negativo) si produce más de 800 unidades. Produciendo exactamente 800 unidades, el beneficio es cero.
Ejercicio 7.1 Cambios en el mercado
Elabora gráficos que muestren cómo cambiarían las curvas de la figura 7.4a en cada uno de los siguientes casos. Para facilitar el trazado de las curvas, supón que la curva de demanda es lineal. En cada caso, explica qué pasaría con el precio y el beneficio de la empresa.
- Una empresa rival, que vende una marca parecida, baja sus precios.
- El coste de producir Apple Cinnamon Cheerios aumenta a 3 dólares por libra.
- Según un estudio del gobierno que se da a conocer en la prensa, los productos de General Mills son más saludables que otros cereales para el desayuno.
-
«Willingness to pay for a flight in space». Statista. Actualizado el 20 de octubre de 2011. ↩















